Игрови модел „Геометрични приключения” в 6 клас

В статията се разглеждат причините, които налагат използването на игрови модел на обучение в 6 клас в раздел „Геометрични фигури и тела”. Статията представя игрови модел на обучение, наречен „Геометрични приключения“, който е разработен за подобряване на учебния процес по геометрия. Разглеждат се целите, структурата и методите, използвани в игровия модел, както и ползите от неговото приложение в образователната среда.

Защо е важно усвояването на геометричните фигури и тела от учениците в училище?

В резултат на изучаването на геометрични фигури и тела учениците

• Развиват визуалното си мислене и пространствената си ориентация: Геометричните фигури и тела са пример за абстрактни концепции, които изискват въображение и пространствена представа;
• повишават математическите си умения: Геометричните фигури и тела са основа за развиването на математически умения, като геометрични преобразувания, измерване на ъгли и страни и решаване на пространствени задачи;
• подобряват езиковите си умения: Изучаването на геометрични фигури и тела изисква употребата на специализирана геометрична терминология, което подобрява езиковите умения на учениците;
• развиват творческото си мислене: Геометричните фигури и тела могат да бъдат използвани за развиване на творческо мислене и решаване на проблеми. Учениците могат да използват геометричните фигури за създаване на нови фигури, тела и модели; подобрява се интегрирането на знанията: Геометрията има много приложения в други науки, като изобразително изкуство, физика, инженерство и архитектура. Изучаването на геометрични фигури и тела спомага за интегрирането на знания между различни науки и предмети.

При изучаването на геометрични фигури и тела в 6 клас учениците срещнат някои трудности.

1. Абстрактност – Учениците трябва да разберат, че геометричните фигури и тела не са реални обекти, а абстрактни понятия. Това може да бъде трудно за тях да визуализират и разберат.
2. Терминология – Има много специфични термини, които се използват в геометрията, които учениците трябва да усвоят и да разберат правилно.
3. Пространствено мислене – Геометрията изисква учениците да мислят пространствено и да разбират отношенията между фигури и тела в тримерното пространство. Това може да бъде трудно за тях да възприемат.
4. 4. Прецизност – Грешки при измерването и чертаенето могат да доведат до грешки в резултатите и разбирането на материала. Учениците трябва да бъдат много внимателни и прецизни.

Тези трудности могат да бъдат преодолени чрез създаване на забавна и мотивираща образователна среда, която да възбуди интереса на учениците и да им помогне да запомнят по-добре учебната материя. А какво по-забавно има от играта?

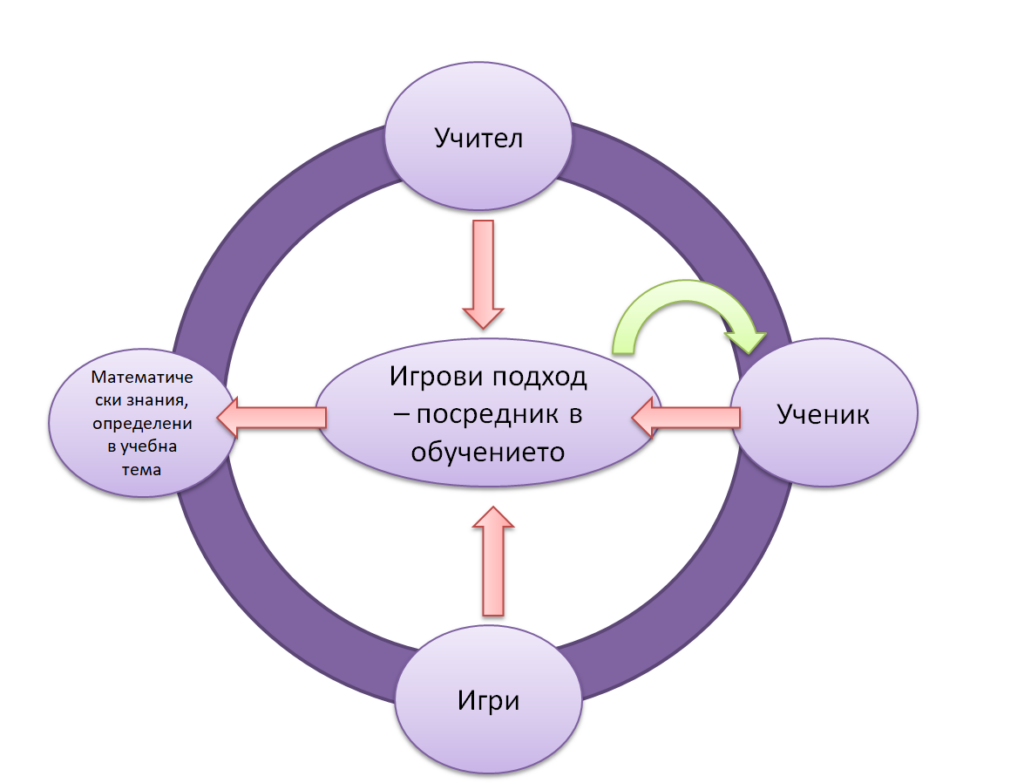
Игровият модел на обучение се основава на идеята, че ученето може да бъде забавно и ефективно. Игрите се използват като средство за постигане на образователни цели. Този метод може да подобри мотивацията на учениците за учене, да развие техните критично мислене, проблемно решаване и комуникационни умения, както и да им помогне да се ангажират по-добре с учебната материя. В този метод обучението се представя като игра, която има определени цели, правила и награди.

Структурата на игровия модел „Геометрични приключения” включва няколко етапа, които да помогнат на учениците да запомнят математическите концепции и да приложат знанията си на практика.

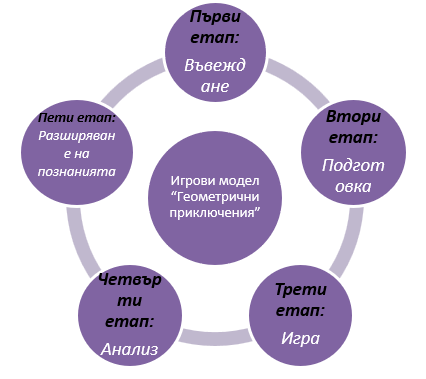
1. Въвеждане: Учениците се запознават с играта и се представят правилата и целта на играта. В този етап, учителят може да представи нови математически концепции, които ще бъдат използвани в играта. Целта на въвеждащия етап е да подготви учениците за участие в игровата среда и да осигури необходимата информация и мотивация, за да се ангажират активно в последващите етапи на игровия модел „Геометрични приключения“.
2. Подготовка: Учениците се подготвят за играта, като учат нови математически понятия, правила или стратегии, които ще им помогнат да играят по-добре. Подготвителният етап е важен за осигуряване на ясност и разбиране на играта от страна на учениците. Той им помага да бъдат готови и подготвени за участие в игровия процес и да постигнат максимална полза и учебен напредък от игровата активност.
3. Игра: В този етап учениците играят играта. Те прилагат знанията си по математика и се съревновават с други участници, като прилагат новите знания в практика. Играта предоставя на учениците вълнуващо и образователно изживяване, като насърчава тяхната активност, мотивация и геометрично мислене.
4. Анализ: Учениците преглеждат играта, анализират своите действия и оценяват своите успехи. В този етап, учителят може да зададе въпроси, за да подтикне учениците да размислят върху своите решения и да ги направят по-добри в бъдеще. Анализът на тези аспекти помага да се разбере ефективността и приложимостта на игровия модел „Геометрични приключения“ в образователната среда и да се направят препоръки за евентуални подобрения или приспособявания според нуждите и целите на учениците.
5. Разширяване на познанията: В този последен етап, учителят предоставя допълнителни ресурси, за да помогне на учениците да разширят своите познанията и разбиране за геометрията, като в същото време да развият геометрични умения, логическо мислене и пространствени представи по конкретна математическа тема, която е била обхваната от играта.

Използването на тези етапи помагат за постигане на по-добри резултати в обучението по математика. Игровия модел „Геометрични приключения” може да бъде много ефективен, когато се използва правилно и когато се комбинира с други методи на обучение.

В игровия модел на обучение „Геометрични приключения” са включени четири игри, които са съобразени с материала, които трябва да усвоят учениците в рамките на раздела „Геометрични фигури и тела”. Първата игра покрива критерия знания. Чрез нея играчите научават геометричните фигури – окръжност, кръг и правилен многоъгълник, телата – призма, пирамида, цилиндър, конус, сфера и кълбо. Усвояват елементите им, затвърждават познанията си за изучените понятия. Идентифицират фигурите и телата в различни контексти и позиции. Втората и третата игра обхващат критериите знания и рецептивни умения. Чрез тях учениците се научават да разпознават и описват фигурите и телата, развиват умения за пространствена представа, визуално въображение и способност за тримерно мислене, затвърждават уменията за работа с линия и пергел (игра 3). Създават умения за интерпретиране на условие и създаване на математически модел. Четвъртата игра е свързана с развиване на продуктивните умения на учениците. Тя предлага геометрични задачи и предизвикателства, които изискват логическо мислене и прилагане на геометрични принципи – пресмятане на периметър, лице и обем, откриване на подобни фигури и други геометрични операции. Затвърждаване на придобитите умения за решаване на права и обратна задача.

Игрите от игровия модел насърчават комуникацията и сътрудничеството между учениците. Засилват мотивацията за учене. Развива пространствени умения. Подпомагат абстрактното мислене Те могат да се играят индивидуално или в група, където трябва да обменят информация, да обсъждат решения и да работят заедно за постигане на обща цел. Това им помага да развият умения за сътрудничество, обмен на идеи и разбиране на различни подходи към решаването на задачи, а материама е представен по-забавен и достъпен начин. Тези причини подчертават важността на игровия модел „Геометрични приключения“ в обучението по математика в 6 клас.

Целта на игровия модел „Геометрични приключения“ е да се стимулира интересът, мотивацията и активното участие на учениците в процеса на учене по геометрия. Чрез въвличането на елементи на игра, предизвикателства и състезателност, моделът създава забавна и вълнуваща образователна среда, в която учениците могат да прилагат и развиват своите знания и умения в геометрия.