6.4. Алгоритъм на анализа на тестовата задача
За анализ на критериално ориентирани тестове прилагаме алгоритъма от фигура 2, където с „в“ сме означили „верен отговор“, а с „д“ – „дистрактор“.
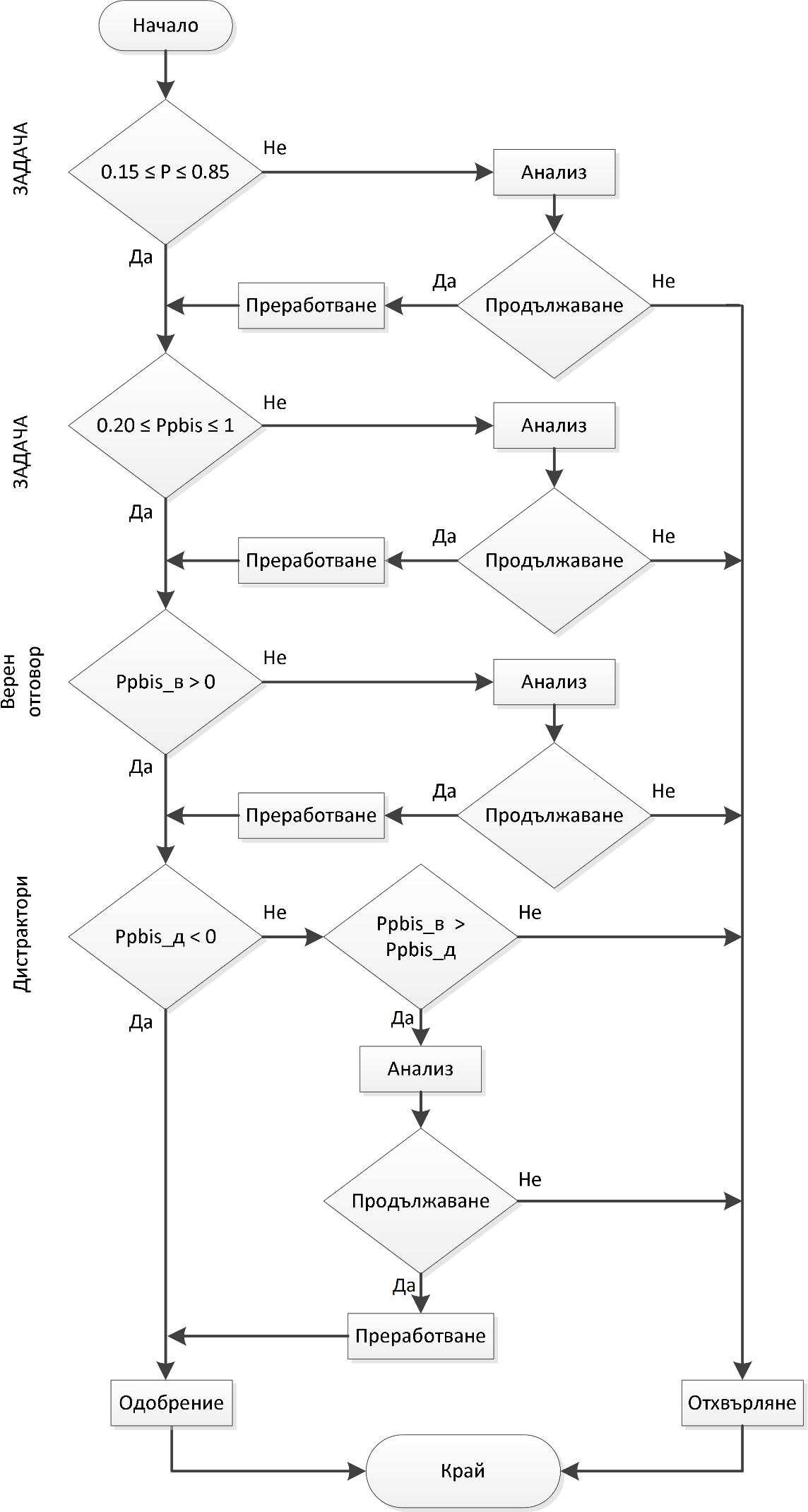
Фигура 2. Алгоритъм за анализ на тестова задача
Спрели сме се на тази последователност от действия и на тези гранични стойности на основните показатели след задълбочено проучване на литературата и на базата на богат личен опит за практическа осъществимост.
Стъпка 7. Преработване на тестовите задачи според резултатите от анализа
В конкретния пример с онлайн теста по ИТ пилотният тест съдържаше близо 160 тестови задачи, които успяхме да редуцираме наполовина в резултат на направения след администрирането му анализ на алтернативите. Много полезни практически съвети са изложени в: Haladyna et al., 2002: 309–334. Други ценни идеи възникнаха след обсъждания с колеги. Процесът е аналогичен на този, описан в Стъпка 4 (Шотлеков, 2011).
Независимо че според някои автори равният брой отговори на въпросите в един тест не му дава психометрични предимства (Frary, 2002: 62), ние предпочетохме всички задачи да бъдат с по четири възможности за избор.
Стъпка 8. Съставяне и провеждане на дидактическия тест
Тази процедура е аналогична на пилотния (предварителния) тест. Едни въпроси отпадат, други се добавят, трети се редактират. Новите попълнения се поставят на подходящо място според спецификацията на теста и според трудността им съгласно прогностичната оценка на преподавателя.
При провеждане на теста трябва да се гарантират стандартни условия, така че да няма облагодетелствана част от тестуваните. Това е особено важно с оглед на психологическия комфорт за равен старт, елиминирането на възможности за измами и пр.
Стъпка 9. Апостериорен анализ
След като бъде проведен тестът, получените резултати се анализират по процедура, подобна на тази в Стъпка 6.
9.1. Надеждност
„Коефициентът на надеждност е число, което показва доколко изменчивостта на наблюдаваните резултати може да се обясни с факта, че тестуваните се отличават един от друг по отношение на характерната черта, която тестът измерва“ (Ebel & Frisbie, 1991: 77–79). Когато това е така, стойността на коефициента на надеждност е висока и близка до единица, а когато е близка до нула, това означава, че различията в резултатите се дължат на случайни грешки, а не на истински различия между участниците в теста.
9.1.1. Методи с двукратно полагане на тестове
Изготвят се два варианта на теста, които са еднакви (паралелни / тест – ретест метод) или еквивалентни.
За да бъдат еквивалентни, те съдържат различни тестови задачи със сходни технически показатели: брой, трудност, коефициент на точкова бисериална корелация и среден тестов бал. Те трябва да са положени от едни и същи студенти (N1 ≡ N2). Коефициентът на корелация между двата еднакви теста трябва да бъде удовлетворителен (напр. над 0.8), при адекватно ниво на статистическа достоверност на резултата (напр. р<0.005).
9.1.2. Методи с еднократно полагане на тест
Методът на разполовяването предвижда разделянето на един тест на две еквивалентни половини, например на принципа четни-нечетни въпроси и пр. След това се пресмята коефициентът на корелация между тестовите балове от двата теста.
Метод на Кудар-Ричардсън
K-R20 e средноаритметичната стойност на корелациите на всички възможни разделяния на теста наполовина (Ebel & Frisbie, 1991: 84). Тази формула е приложима, ако задачите се оценяват по критерий вярно-невярно, като за верен отговор се отсъжда 1 точка и 0 точки – за погрешен.
Коефициент α. С него могат също така да се оценяват и скали на Ликерт, задачи с отворен отговор и пр. Ако тестът се оценява дихотомно (с две категории – вярно-невярно), стойността на α съвпада с K-R20.
При нормативно ориентирани тестове може да се направи следното тълкуване на коефициента алфа: α>0.9 – Отлично, α>0.8 – Добре, α>0.7 – Приемливо, α>0.6 – Под въпрос, α>0.5 – Слабо, а α< 0.5 – Неприемливо (George & Mallery, 2003: 231). Когато един критериално ориентиран тест измерва няколко отделни умения, например с по 10–15 въпроса за всяко от тях, коефициентите на надеждност за всеки от подтестовете ще бъдат определено по-ниски поради по-малкия брой въпроси и трябва да се съобщават поотделно за всеки от подтестовете (Popham, 1978: 94).
9.1.3. Определяне на стандарта за успешност
При критериално ориентираните тестове е важно да се определи стандартът за успешност, който разделя обучените от необучените. В литературата са описани няколко метода, а тук ще се спрем на метода на граничните групи, познат още като метод на контрастните групи, който се препоръчва при тестове с множествен избор. Първата стъпка е да се изберат експерти по учебното съдържание, които да отсъдят принадлежността на тестуваните към една от две контрастни групи – силна и слаба. Построяват се диаграми с честотните разпределения на представителите на двете групи и пресечната точка на двете графики определя стандарта на успешност, напр. 67%. Във всяка от групите трябва да има поне 15 души, а за предпочитане 30 или повече (Shrock & Coscarelli, 2007: 279). Разбира се, има значение и диапазонът на скалата с възможните тестови балове, защото разпределението на резултатите на трийсет души (2×15) ще бъде различно при два различни теста, единият от които има 10 въпроса, а другият – 100 например.
