Стъпка 10. Нормиране
10.1. Стандартизиране на резултатите
Един суров бал е труден за интерпретиране, защото зависи от дължината на теста, от сложността на въпросите и от грешката на измерването.
За отправна точка използваме честотното разпределение на резултатите, което онагледяваме с хистограма и в таблица с подредения във възходящ ред суров бал за всеки тестуван, заедно с честотата, с която се среща всеки от баловете, процента на честотата на дадения бал, както и валидния и кумулативния процент (фиг. 3а).
Като тест за нормалност може да послужи отношението на коефициента на ексцес (Kurtosis) към неговата стандартна грешка (Standard Error of Kurtosis), както и отношението на коефициента на асиметрия (Skewness) към неговата стандартна грешка (Standard Error of Skewness), вж. оградените от нас с елипса на фигура 3б. Може да се приеме нормалност, когато отношението е в диапазона от -2 до +2. Резултатите от фигура 3в са получени с помощта на PSPP, който е много удобен за ползване със своя графичен потребителски интерфейс.
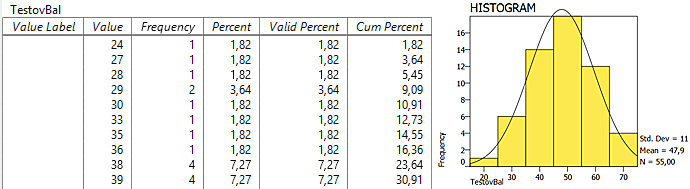
а)
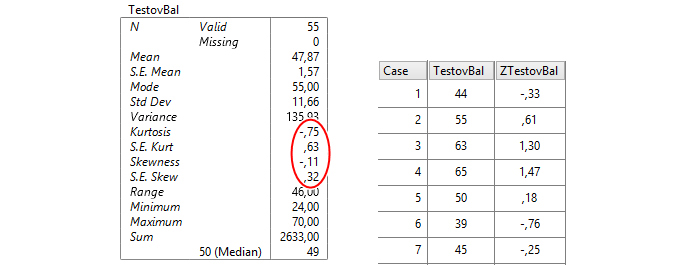
б) в)
Фигура 3. Честотно разпределение (а), изследване за нормално разпределение (б) и стандартизирани стойности (в) на тестовия бал с PSPP
Изчисляваме стандартизираните стойности (z-score) за всеки от резултатите, които са особено информативни при нормално разпределение на изходните данни. Те позволяват сравнение на относителното класиране на обучаеми при различни средни балове или с различни стандартни отклонения. Ако z=0, този бал се намира точно в средата на разпределението и е равен на средната стойност; ако z=1, този бал се намира на едно стандартно отклонение над средната, а при z= -1 той е на едно стандартно отклонение под средната стойност (вж. фиг. 3в).
