В статията се проследява връзката на съвременните параметри на математическата наука и учебна дисциплина с откритията на древните математици и философи. Разкрива се математическата фантазия на природата. Оценява се голямата роля на науката математика в развитието на човешката цивилизация. Определя се преходът от нагледно-образно към логическо и абстрактно мислене. Предлагат се интересни примери и доказателства за връзката на математиката с бита и обществото. Акцентира се върху космополитната значимост на математическата наука. Отбелязва се свързаността между човешките чувства и усещане за красота. Посочени са примери за хармонията в математиката, за нейната фундаменталност и приложна значимост. Математиката е разгледана като провокатор на мисленето и развитието на уменията на учениците.
Освен методически добре подготвени, учителите трябва да знаят какво мотивира и интересува техните ученици. В търсене на иновативни практики и подходи в обучението по математика да се върнат към началото на науката, преди хилядолетия.Съвременните хора все още измерват ъглите по 360-градусова система, въведена от вавилонците. Все още следват принципите на древногръцката геометрия. Използват се алгебричните алгоритми на маврите. През по-голямата част от историята на човечеството, математиката е свързана с конкретни неща. В древността тя е използвана чрез предмети, количества, теглене, строителство. Предкласическите народи на Вавилон, Египет и Индия притежавали умението да сравняват по размер и количество и имали завидни умения да определят пропорции. После това умение се развило до способността да броят. Днес това ни се струва изключително елемнтарно математическо познание, но хилядолетия назад във времето, това е било въпрос на развита мисловна дейност. На по-късен етап започва използването на количиствени, качествени понятия. Количествените понятия се утвърждават на по-висша, абстрактна степен на мисленето. А истинска революция е появата на понятието число .
Древни египетски папируси ни дават сведения за първите математически текстове. Най-големият математически текст от онова време съдържа 84 задачи. Папирусите са били създадени с учебни цели като основно внимание се отделя на методите за решаване на задачите, а не на самото пресмятане. Задачите, описани в най-големия документ-Папирус на Райнд са обхващали задачи за обем на хамбари или задачи за определяне на площи. Смятането било просто и се свеждало до умението да се събират числата. Някои изследователи твърдят, че за математиката не е нужно нищо повече от елментарна аритметика и нормален здрав разум. (Баптист 2017) Още тогава хората са имали нужда от външна опора при запаметяването. Използвали дребни камъчета, раковини, цветни възли. Тези възли били доста сложна система, особено при инките. Прочутите кипу/ възли по разноцветна връв/ представляват различни числа, взависимост от броя на пресукванията на влакното или възлите по него. Счетоводителите на инките с тази бройна система успявали да съхранят и боравят с информация за данъци, приходи, календар, обработваеми площи.
Нагледно-образното мислене в древността е последвано от абстрактното математическо мислене. На територията на Централна Африка е открита кост, датирана от преди 25 хилядолетия, която има нарези, групирани по специфичен начин. Те били подредени по 60 в два реда. Според известин американски археолог, това не е бройна система, а лунен календар за фазите на луната за шест месеца. Някои изследователи смятали, че това е календар за отбелязване месечния цикъл на жена. Все твърдения от гледна точка на нашето съвремие, но в същото време доказателство за древен тип математическо мислене.
Нагледните помагала за разбиране и запомняне не са от вчера. Те датират от древността. В Древен Египет е било използвано Окото на Хор. Помагалото е използвано за запомняне на дробите ½, ¼ , 1/8 и т.н. Елементите на окото са били обозначени и като дроби. Според един от митовете Сет разкъсал окото на шест части. На всяка от тях съответства мярка:
| 1/2 – дясната страна на окото, | 1/16- лявата страна на окото, |
| 1/4- зеницата, | 1/32-извитата опашка, |
| 1/8- вежда, | 1/64-сълза. |

Тези части се равняват на 63/64, а липсващата част или се казва, че представлява магическата сила на Тот, или за да покаже, че нищо не е съвършено.
Математиката от древността до наши дни изумява хората със своята уникалност, но и приложимост. Тя е съвършена композиция от наука и изкуство. Тя е хармония и духовна насада.
Докато са в училищна среда и възраст, децата по правило приемат неизбежността на учебния процес и рядко вникват в дълбокия смисъл на науката математика. Става въпрос за реалните, общесвени училища, в които се обучава голяма част от подрастващите. Онези ученици, които нямат изявени способности и подчертан математически интерес. На по-късен и осъзнат етап в развитието, младите хора изкраждат по-висока мотивация са себеосъвършенстване и това води към търсения и открития, които изграждат общата куртура на личността. Това се отнася и за математическата наука.
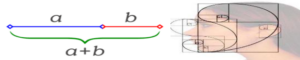
Много от нас откриват интересни математически открития едва, когато са в зряла възраст. Например, голяма част от хората се очароват от идеята за златното сечение и неговата проява в геометрията и архитектурата. Числото, наречено “златно сечение” се появява и в книгата “ Шифърът на Леонардо”, в много статии и книги, които имат за цел да покажат значимостта на математиката в реалния свят. Терминът е въведен от Леонардо да Винчи. Много автори го описват като божествена пропорция на красиви модели в природата. Изследователи и наблюдатерли твърдят, че в много от шедьоврите на изкуството и архитектурата се съдържат елементи и пропорции, съгласувани със златното сечение. За примери се посочват храмът Партенон и Египетските пирамиди. Дори се твърди, че тази божествена пропорция ясно личи в човешкото тяло. Същността на златното сечение е представена от древногръцкия математик Евклид. Ако трябва да се раздели отсечка на две части и съотношението между целия сегмент и по-дългото от двете парчета е същото като съотношението мужду по-дългото от двете парчета и по-късото, то какво ще бъде това съотношение? По дефиниция златното сечение е ирационално число, което изразява отношение на части, при което по-голамата част се отнася към по-малката така, както цялото към по-голямата. Това число има приблизителна стойност от 1,618. Число, което е символ на красотата и хармонията в изкуството, науката и природата.
Древните египтяни и древните гърци със своите архитектурни паметници показват приложимостта на златното сечение хилядолетия назад. В Средновековието също може да бъде открит пример за златно отношение. На фасадата на катедралата Парижката света Богородица се вижда как всеки архитектурен елмент се отнася към някой от останалите в златно сечение.
Ретроспективната разходка в миналото ни дава своебразна представа за космополитната значимост на науката математика. Приложимостта на законите и принципите на математиката правят учебната дисциплина изключително значима при изграждането на фундамента на човешкото познание. Математиците обичат математиката, заради нейната предизвикателност и красота. Математиката гледа от природата, ние гледаме от математиката.
Една от най-често срещаните фигури в природата е шестоъгълникът. В него се открива универсално съотношение между отделните елементи, което създава усещане за съвършена хармония и красота. Теорията за съвършения шестоъгълник се представя и доказва чрез медената пита, снежинките и капките вода- хармонично съчетание между стотици малки шестоъгълничета.
Математическите изчисления все повече се използват в новите технологии, в медицината и молекулярната биология. Според теорията за фрактален природен алгоритъм, при голяма част от растенията, увеличението на техните размери се дължи на увеличението на отделните им съставни елементи, които са с абсолютно еднаква структура. От стъблото излизат разклонения, а по тях нови листа, пъпки и цветове, които са едни и същи с основните. Тези повтарящи се многократно елементи се наричат фрактални. Този процес изключително наподобява процесът на разклоняване на кръвоносната система в човешкото тяло. Това безкрайно почти повторение е категорично изразено в папратите. (Милева 2022)

Има много причини непознаваемата природа на математиката да бъде близо до магията. Геометричната теорема, наречена Парадокса на Банах-Тарски, гласи, че ако имаме топка в триизмерното пространство и тя се раздели на няколко конкретни части, то има начин да се съберат отново частите , така че да се създадат две топки. Но странното е, че създадените две нови топки могат да бъдат със същия размер като първата. Според теоремата е възможно да се сглобят отново парчетата по начин, който удвоява топките. Удвояването противоречи на логиката на реалния живот, то е само математически възможно.

Доктор Томас Бриц споделя: “За да усетите много красиви части от математиката, имате нужда от много основни познания. Имате нужда от много основни и често много скучни тренировки. Но си заслужава. Надявам се, че повече хора ще стигнат до забавната част от математиката. Има толкова много красота за разкриване.” (Милева 2022)
Красотата на математиката остава тайна за много деца в училище. Те виждат в нея само мъчни уравнения и неясни формули, които не свързват с приложимостта им в реалността. Математическите умения са талант, който малцина притежават. За голямата част ученици успехите в часовете по математика се постигат с много концентрация, упоритост и упражнения. Няма как да повлияем на природните предимства, но бихме могли да направим достъпна и желана математическата дисциплина за повече ученици.
Посочените примери за връзката на математиката с природата и хармонията не изчерпват нейната фундаменталност и приложимост в живота ни. Информацията за универсалността на науката математика е важно да съпътства дидактическия материал. Така учащите ще установят връзката между закономерностите в науката и приложимостта на математическите алгоритми. От методическа гледна точка това е значимо за мотивацията и успеваемостта на ученика.
Математическите теории и задачи са провокатор на критично и логическо мислене, но и на чувствата и естетическите възприятия. Математиците приличат на поетите и художниците, на композиторите и архитектите, защото са виртуорни създатели на мотиви, структури, модели, в които има мъдрост и живот. Красотата на математиката не зависи от степента на трудност, нито от равнището на резултатите. На елементарно ниво тя може да има високо естетско съдържание. Истинското приключение е прилагането на математически умения. Истинско приключение е прилагането на математическите умения. То изисква съообразителност и последователност. (Баптист 2017)
В началното образование е важно децата да се докоснат до съвършенството и магичността на математическите принципи и да визуализират тяхното приложение в заобикалящата ни реалност. Затова предлагането на учебния материал в атрактивен формат трябва да е приоритет на педагозите и авторите на учебни материали. Новите ИКТ подобряват качеството на образованието. Чрез тях децата се чувстват по-ангажирани, развиват нови, полезни умения. Ако учителите се придържат към видимата красота на математиката и покажат нейния скрит магнетизъм, учениците ще се мотивират повече в учебния процес и ще постигат по-високи резултати.
