РЕЗУЛТАТИ ОТ ПЕДАГОГИЧЕСКО ИЗСЛЕДВАНЕ ЗА РАЗВИТИЕ НА МАТЕМАТИЧЕСКИТЕ ПРЕДСТАВИ ПРИ 6–7-ГОДИШНИ ДЕЦА

В статията са разгледани целта, задачите и хипотезата, както и нейното доказване, за проведено педагогическо изследване за изграждане на математически представи у 6–7-годишните деца в условията на детската градина. Коментират се етапите на експеримента и специфика на развитие на децата от четвърта възрастова група и периодът на предучилищната възраст. В контекста на отношенията актуални са понятия за: „Вариационен анализ“; „Персантален анализ“; „Алтернативен анализ“. Акцентът е поставен върху математико – стастистически методи за обработка на данните от изследването. Направени са важни изводи и препоръки за бъдеща работа.

Въз основа на анализа на специализираните източници, както и актуалността на проблема, съобразно приложението на приказния жанр, творческата игра, продуктивната дейност и играта на децата в образователния процес по математика в условията на детската градина, са формулирани следните цели, задачи, хипотеза, предмет и обект на експерименталното изследване за развиване на математически представи:

Цел: Да се разработи и апробира експериментално дидактичен модел за стимулиране на процеса на изграждане на математическте представи у 6–7-годишни деца.

Задачи:

1. Да се проследят и установят знанията и уменията по математика на 6–7-годишните деца на констатиращия и на контролния етап от експеримента, чрез дидактични тестове за проследяване на постиженията им.
2. Да се разработи и апробира на обучаващия етап от експеримента дидактичен модел за стимулиране на математическите представи у 6–7-годишните деца, чрез приложение на приказния жанр и творческите  игрови дейности, който се прилага на обучаващия етап на експеримента.
3. Да се докаже хипотезата на експерименталното изследване.

Хипотеза: Предполага се, че ако се разработи и апробира подходящ дидактичен модел за изграждане на математически представи у 6–7-годишни деца, съобразен с възрастовите и индивидуалните  особености на изследваните лица, методиката за изграждане на елементарни математически представи и приложението на приказния жанр, чрез игрови и практически ситуации, може да се очаква разширяване  и  затвърдяване на математическите знания и умения на децата и стимулиране на интелектуалното  им развитие, формиране на познавателни и творчески способности.

Предмет: Целесъобразност и ефективност на знанията и уменията по математика чрез приложението на приказния жанр.

Обект: Процесът на формиране на умения у децата да се ориентират в количествени, времеви, пространствени отношения между обекти, разпознават, моделират, възпроизвеждат геометрични фигури, възприемат събирането като практическо добавяне, а изваждането като отнемане на част от група, сравняват обекти по техни признаци: дължина, височина и ширина, познават предназначението на часовника като уред за измерване на времето в игрови и познавателни ситуации.

Етапи на експерименталното изследване:

Първи етап: Констатиращ етап – установяване ниво на математическите представи на децата преди обучаващия етап на експеримента.

Втори етап: Формиращ  етап – апробиране на система от форми на педагогическо взаимодействие в условията на детската градина (игрово – познавателни ситуации по образователно направление математика за четвърта възрастова група) чрез приложение на приказки.

Трети етап: Контролен етап – установяване продуктивността на приложените методически инструменти, анализ и обобщаване на получените резултати след обучаващия етап на експеримена.

Обхват:  Изследвани са 28 психически и физически здрави деца на възраст шест и седем години от четвърта възрастова група “ в ОУ “ Св. св. Кирил и Методий“, гр. Кюстендил в периода октомври  2021 г. – май 2022 г.

Математико – стастистически методи за обработка на резултатите

За обработка на резултатите от изследването се използват математико- стастистически методи, чрез които проверяваме наличието на взаимовръзката между две величини и повече величини от изследваната област, сравняваме средни показатели на няколко зависими променливи, проверяваме верността на хипотезата, силата на взаимовръзката между определени величини и други.

Вариационен анализ

Вариационният анализ, наричан още параметричен, дава основни статистически показатели. При него важна роля имат параметрите: средна аритметична величина и стандартно отклонение. Чрез средната аритметична величина се измерва средното ниво на признака, притежаван и измерван за всяка единица от  подложената на наблюдение група. Показателят се явява като обобщена характеристика на цялата група по отношение на изучения признак.

Цел: Да се изведе средно аритметично от индивидуалните постижения на децата.

Начин на изчисляване: Коефициентите на всички деца се събират и се делят на  броя на децата в групата /n/.

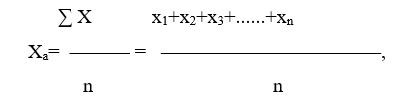
където:

Х_a  е средна аритметична величина;

х₁,х₂,х₃……,х_n  – определенията по вариационен признак (точките на децата);

n     – броят на осредняваните величини;

∑  – знак за сбор

Персантален анализ

Цел: Групиране данните в персантили

Инструментариум: Персантили, които включват следните означения:

– Брой деца с ниско равнище

– Брой деца със средно равнище

– Брой деца с високо равнище

Начин на изчисляване: Определя се среден коефициент. Данните се изчисляват в проценти (%) и се изнасят в таблица.

Брой деца с ниско равнище	Брой деца със средно равнище	Брой деца с високо равнище

Алтернативен анализ

На базата на получените емперични данни от изследването се извършва обработка чрез алтернативен анализ, т.е изчислява се в процентно отношение броя на изследваните лица, принадлежащи към съответната категория. Резултатите се приравняват в процентно отношение по формулата: Брой деца с верни отговори

         общ брой деца с верни отговори
% =  —————————————————————  x100
        общ брой деца, участвали в изследването

 Графични методи

За по-голяма нагледност резултатите на изследваните деца се представят в табличен и графичен вид. Графичните методи позволяват чрез графи, диаграми, пространствени изображения и други визуални форми да се представят параметрите на резултатите.

Доказване на хипотезата –  метод на Стюдънт

За докзване на хипотезата от експиременталното изследване е  използван

 t-критерий на Стюдънт, който дава възможност да се съпостави признак (нивото на усвоеност на математическите знания на изследваните деца), измерен в една и съща група, но в различни условия ( преди и след обучението с дидактичната технология).

Етапите на проверка на статистическите хипотези включват следните дейности [1] :

1. Определяне на нулева ( Н₀) и алтернативна (На) хипотези на проверката.
2. Избиране на критерий за проверка на нулевата хипотеза.
3. Определяне на нивото на статистическа значимост на проверката – обикновено в педагогическите изследвания се приема 0, 05 или 5%. Това означава, че направеният извод е с 95% сигурност.
4. Пресмятане на стойността на проверяващата величина.
5. Определяне на критичната област – област от значение на изчисляваните величини, за която закономерността, положена в основата на съответния статистически метод, не важи. Използват се таблици.
6. Вземане на решение относно статистическата основателност на нулевата хипотеза.

Ако tизч< tα, то за вярна се приема нулевата хипотеза.

Ако tизч> tα, то за вярна се приема алтернативната хипотеза

Анализ на резултатите от констатиращия етап на експеримента

Равнищата за проследяване на постиженията на децата в направление „Математика“- входящ мониторинг са нанесени в Таблица 1.

Таблица 1. Протокол на изследваните деца за развитие на математически представи – входящ мониторинг

 

№	точки	Равнища на постижения
1	49	високо
2	48	високо
3	45	високо
4	35	средно
5	37	средно
6	38	средно
7	37	средно
8	34	средно
9	29	средно
10	26	средно
11	26	средно
12	33	средно
13	38	средно
14	38	средно
15	37	средно
16	28	средно
17	24	ниско
18	24	ниско
19	21	ниско
20	22	ниско
21	25	ниско
22	17	ниско
23	25	ниско
24	25	ниско
25	22	ниско
26	23	ниско
27	25	ниско
28	23	ниско

 

Данните са групирани и обобщени в Таблица 2 и са онагледени в Диаграма 1.

Таблица 2. Обобщен протокол за равнищата на постиженията на изследваните

лица в началото на учебната година

 

Равнища на постиженията на математически знания	Брой деца	%
ниско равнище	12	43%
средно равнище	13	46%
високо равнище	3	11%

 

Равнища на постиженията в началото на учебната година

 

Диаграма 1.  Равнища на постиженията на изследваните лица

в началото на учебната година

 

Данните сочат, че при 11% (3 деца) се отчита високо равнище на постижения на математически знания, 46% (13деца) –  средно равнище, 43 % (12 деца) – ниско равнище.

Констатира се, че най-големи затруднения децата са срещнали със задачи, свързани с количествените отношения и пространствена ориентация.

Методически изисквания за провеждане на игрови и познавателни ситуации по математика на формиращия етап от експеримента

Дидактическата технология за стимулиране на математически представи чрез приложение на приказния жанр е съобразена с възрастовите характеристики на децата от предучилищна възраст и критериалните изисквания на ДОС за предучилищно образование.

Методиката е съобразена  и с педагогическите принципи за спираловидност, последователност, научност, индивидуален подход и други.

В педагогическите ситуации за овладяване на елементарни математически представи, съобразно конкретната цел и задачи на експерименталното изследване, бяха използвани различни приказки. Познавателните задачи са компилация от концептуалните идеи на познавателните книжки по математика за четвърта възрастова група на програмната система „Моите приказни пътечки“.

Основно дидактично изискване е включване на детето в собствена дейност с математическа насоченост на практическа, игрова и познавателна основа. Изграждането, разширяването и надграждането  на детските представи за количествените, пространствените, времеви отношения и геометричните фигури се реализираха в забавни и увлекателни практически и игрово – познавателни ситуации чрез логически игри и занимателни упражнения.  Запознаването с графичните белези на числата  се реализира чрез подходящи психомоторни упражнения на базата на конкретна приказка, в която присъстват числа. По този начин се стимулираше развитието на зрително – моторната координация на бъдещите ученици.

Децата формираха умения за броене, моделиране на множества; запознаха се със сезоните и промените, които протичат в живата природа; формираха представи за частите на денонощието, представа за конкретни уреди за измерване на времето – часовник; ориентираха се в лабиринт и т.н.

Формиращият етап от изследването протече в периода от м.октомври 2021 г. до м.май 2022 г., по време на който се изпробва моделът на обучение с децата от експерименталната група. Темите са общо 16 на брой, предвидени за провеждане като задължителни нерегламентирани педагогически ситуации със средна продължителност 30 минути в рамките на 24 седмици, допълнително към регламентираните по програма ситуации. В темите от експерименталния модел бяха включени разнообразни задачи под формата на игри и упражнения за развиване на елементарни математически знания и умения, свързани с конкретна приказка. Прилагането на приказния жанр в ситуациите по математика стимулира познавателната активност на децата и действайки с него, те овладяха  по-плавно и осезаемо определени математически представи и отношения. Дейностите се осъществяваха не само индивидуално от всяко дете, но и групово. Педагогическото взаимодействие се основаваше на субект – субектната форма на общуване, като в центъра на образователния процес бе поставено детето, а не самият модел на обучение.

Комбинирането на двете образователни направления – Математика и Конструиране и технологии в педагогически ситуации  имаше за цел да докаже своя благоприятен ефект върху развиването на математическите компетенции при 6–7-годишните деца. Ролята на дидактичния конструктивен материал е ключова за протичането на дадена математическа ситуация. Благодарение на идеята, която е заложена в него, може да се стимулира детската инициативност и да се постави акцент върху уменията за анализ и стремеж към изява.

Апробираната дидактическа технология  е доказателстово, че чрез приложението на приказките в образователния процес по математика в условията на детската градина може да се преодолее противоречието между абстрактността на математиката като наука и конкретността и образността на детското мислене и води до  по-високо равнище на усвоените знания.

Анализ на резултатите от контролния етап на експеримента

Равнищата за проследяване на постиженията на децата в направление „Математика“- изходящ мониторинг са нанесени в Таблица 3.

Таблица 3.  Протокол на изследваните лица за развитие на математически представи-изходящ мониторинг

 

№	точки	равнища на постижения
1	60	високо
2	60	високо
3	59	високо
4	57	високо
5	58	високо
6	56	високо
7	56	високо
8	55	високо
9	54	високо
10	52	високо
11	50	високо
12	54	високо
13	56	високо
14	57	високо
15	56	високо
16	47	високо
17	48	високо
18	47	високо
19	44	средно
20	40	средно
21	46	високо
22	20	ниско
23	46	високо
24	45	високо
25	44	средно
26	44	средно
27	45	високо
28	43	средно

 

Данните са групирани в  Таблица 4 и са онагледени в Диаграма 2.

Таблица 4. Обобщен протокол за равнищата на постиженията на изследваните лица в края на учебната година

Равнища на постиженията на математически знания	Брой деца	%
ниско равнище	1	4%
средно равнище	5	18%
високо равнище	22	78%

 

Равнища на постиженията в края на учебната година

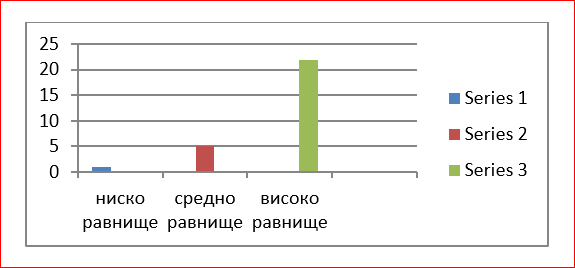
Диаграма 2.  Равнища на постиженията на изследваните лица

в края на учебната година

Данните сочат, че при 78% (22 деца) се отчита високо равнище на постижения на математически знания, 18% (5 деца) –  средно равнище, 4 % (1 дете) – ниско равнище.

Констатира се, че чрез приложената дидактическа технология децата повишиха знания, умения и отношения по математика .

Обобщени резултати от равнища на постижения в началото  и края на учебната година са групирани в  Таблица  5  и са онагледени в Диаграма  3.

Таблица 5. Обобщени резултати

Период на изследването	Равнища на постиженията – %
	ниско	средно	високо
преди обучението	12-43%	13-46%	3-11%
след обучението	1-4%	5-18%	22-78%

Обобщени резултати

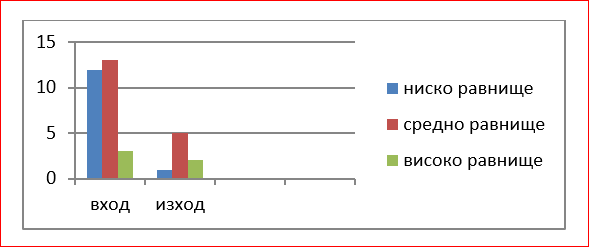
Диаграма 3. Обобщени резултат

Доказване на хипотезата: чрез t – критерий на Стюдънт

Интересуваме се дали след проведено обучение се е подобрило нивото на развитие на матматически представи и умения при децата.

Нулева хипотеза Н₀ – Не съществува статистически значима разлика (зависимост) между получените резултати на входното и изходното ниво след приложение на приказния жанр в процеса на обучение (игрово – познавателните ситуации ).

Алтернативна хипотеза На – Между изследваните характеристики на входното и изходното ниво се наблюдава статистически значима разлика (зависимост) и тя се дължи на приложението на приказния жанр в процеса на обучение.

За проверката на хипотезите  се сравняват разликите между средните величини. Според този метод, нулевата хипотеза се приема или отхвърля в зависимост от получената разлика т.е.

Н₀: ако x_{0 =} x;  На: ако x₀ ≠ x;

Определяне на вида на разпределението.

Коефициент на вариация  вход –

Коефициент на вариация  изход  –

Извадката е с малък обем n ≤ 30, затова ще приложа  т. нар. t-разпределение или разпределение на Стюдънт. Легенда:

– средна аритметична величина от данните, получени от изходното измерване (тест…)

– средна аритметична величина от данните, получени от входното измерване (тест…)

 – стандартно отклонение от първото измерване

n – брой ученици/деца (в случая 28)

t-разпределение  вход:

t-разпределение  изход:

Критичната област на хипотезата (област на отхвърляне на На) е двустранна поради двупосочното неравенство, дефинирано в Н₀.  Табличната стойност, ще се определи при избрания риск за грешка (5%), двустранна критична област и  степени на свобода Φ = n – 1= 27, ниво на статистическа значимост α = 0,05 или квантил от порядък 0,95 (степен на сигурност на резултата). От таблицата   е 1,7033 за t-разпределението т.е.

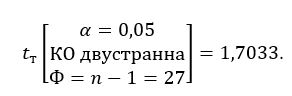
Тъй като
,  то е валидна нулевата хипотеза: Между изследваните характеристики на входното и изходното ниво не съществува статистически значима разлика (зависимост) и тя се дължи на:

• разлика в броя на задачите във входящ /17 / и изходящ мониторинг/20/

Обобщението и анализът на резултатите, получени по време на провеждане  на експеримента, показват следните изводи:

1. Използването на игрови и познавателни ситуации по математика постигна по-високо равнище на усвоените знания и активизиране на познавателната дейност на децата.
2. Създадените дидактически материали водят до повишаване на качеството на знанията.
3. Разработената методика може да бъде използвана и в други образователни направления.
4. Наблюдава се силна мотивация у децата за постигане на максимални резултати.

За по-добро възприемане на обучението по математика в детската градина може да се обобщи, че е необходимо подходящо изложение на информацията и добра визуализация, поради предимно нагледно-образното мислене на децата в предучилищна възраст. Необходимо  е заниманията да се поднасят с игрови акцент, който по непринуден начин да събужда детското любопитство и желание за взаимодействие. Чрез познати приказки и любими приказни герои децата по-успешно  овладяват съответните математически представи.