Приложение на технология за усвояване на учебното съдържание от раздел „Геометрични фигури“ по матeматика в 5. клас чрез използване на подхода „самостоятелно учене“

В статията е представено практическото прилагане на технология за усвояване на учебното съдържание от раздел „Геометрични фигури“ в 5 клас. В изложението е описана концептуалната рамка на иновативната технология, представени са процесите, дейностите, техниките и технологичните решения, които влизат в модела. Отделено е място на съдържателната рамка на технологията за усвояване на учебното съдържание от раздел „Геометрични фигури“ по математика в 5 клас, която представя елементи от модифицирани преговорни уроци на три групи фигури които се изучават в 5 клас с имплементирани задачи за самостоятелно учене в тях. Представени са резултати от педагогически експеримент верифициращ модела чрез реално изследване на две групи ученици от две училища в Северозападна България. Получените резултати са обобщени в изводи показващи значението на технологията за подобряване на усвояемостта на учебното съдържание от раздел геометрични фигури в 5 клас.

1. Концептуална рамка на иновативна технология за усвояване на учебното съдържание от раздел „Геометрични фигури“ по математика в 5 клас

Идеята на модела е свързана с прилагане на подхода самостоятелна работа към класно-урочната форма на преподаване на материала от тематичния раздел „Геометрични фигури“ в 5 клас. Вграждането на няколко „упражнения“ (задачи) които са типични за самостоятелната работа в 3 урока, които се отнасят до най-трудните за разбиране и усвояване нови знания ще допринесе за качествено по-добро ниво на усвояване на новите знания и значима промяна на отношението на учениците от 5 клас към тематиката (геометрични фигури).

Целта на модела е да се приложи на практика обоснована и ефективна технология за самостоятелно учене за учебния материал от уроци за затвърждаване на знанията, която да може да се измерва с ясни и относително прости критерии и показатели. Като резултат при постигане на целта ще имаме на разположение апробиран инструмент (Технология за усвояване на учебно съдържание в раздел „Геометрични фигури“ базирана на подхода самостоятелно учене). В основата на модела е статията на Петер Баптист „Да почувстваме математиката“, която е част от книгата „Към нов  подход в математическото образование“ (преведена е част от нея и издадена под името SINUS and SINUS-Transfer от издателство „Регалия 6“ през 2012 г.).

Основната логика на настоящия модел се състои в следната предполагаема зависимост между последователни съждения:

1) Учениците от  5  клас  имат  сравнително  ниски  постижения  от  раздел „Геометрични фигури“, който е основна част от учебното съдържание на учебния предмет „Математика“;

2). Ключовите причини за ниските постижения на учениците са вероятно: ниска мотивация за учене и усвояване на знания и умения необходими за решаване на задачи от раздел геометрични фигури (тази ниска мотивация е поради това, че не виждат връзка на тези знания с реалността); липсата на подкрепа и стимули от родителите към своите деца – да се заемат по-сериозно с подготовка по математика (защото и родителите не осъзнават значението на математиката и по-конкретно знанията и уменията които се придобиват от предвиденото съдържание в раздел „геометрични фигури“);

3) Подхода „самостоятелно учене“ съдържа в себе си мощен потенциал да промени личната мотивация на учениците да усвояват знания умения и компетентности по математика и по конкретно от раздел „геометрични фигури“;

4) Подхода „самостоятелно учене“ може да бъде имплементиран в урочната форма на преподаване на уроци за нови знания и в упражненията от раздел „Геометрични фигури“ като това става с детайлно описание на иновативен модел представляващ технология за ефективно усвояване на съдържанието от раздел „геометрични фигури“, съдържаща: алгоритъм, дейности по отделни етапи, техники да работа на учителя и на учениците;

5) Създаването и детайлното описание на Модел за ефективно усвояване на съдържанието от раздел „геометрични фигури“ в 5 клас има адекватна теоретична основа (подхода „Самостоятелно учене“) и достатъчно емпирични потвърждения, че този подход работи успешно при преподаването на математика (Баптист 2012,  Георгиева 2015);

6) Верифицирането на модела може да стане с метода: педагогически експеримент (с три етапа) приложен на две групи ученици (експериментална и контролна) , като за целта се разработва система от критерии и показатели и се структурира постановка на изследването със зависима и независима променлива и инструментариум за оценка на постиженията на учениците (тестови метод);

7) Осъществяването на педагогическия експеримент може да стане в рамките на часовете за упражнения от учебната програма по математика (раздел Геометрични фигури) 5 клас).

 

В описанието на модела (иновативна технология за усвояване на учебното съдържание от раздел „Геометрични фигури“ по математика в 5 клас) е включена:

съдържателната и процесуална част. Представени са: процеси; дейности; техники; технологични решения

Моделът е представен графично на следващата фигура 1.

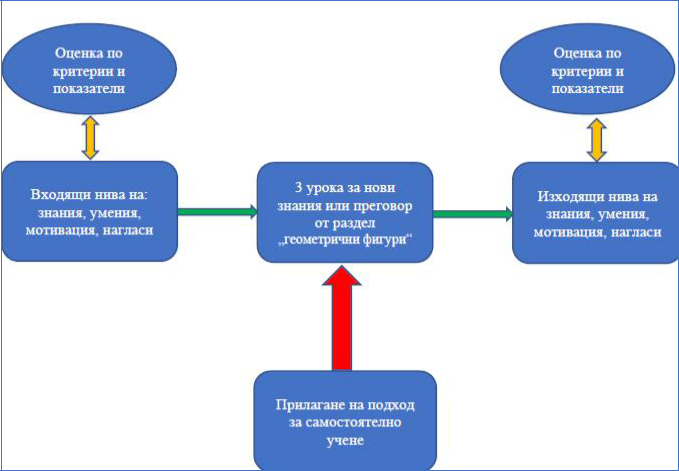Фигура 1. Модел за подобряване на усвояването на учебно държание по математика (геометрични фигури) в 5 клас основан на подхода „самостоятелно учене“

 

1. Процеси
   В процесите които се включват в модела отбелязваме: процес на първоначална оценка на знания, умения, мотивация и нагласи по предварително създадени: чек-лист и анкетна карта; обучение по стандартни обичайни методи на контролната група; обучение  по   модифицирани  3   бр.   уроци   с   включени   елементи   от подхода за самостоятелно учене; финална оценка на знания, умения, мотивация и нагласи по предварително създадени: чек-лист и анкетна карта.

2. Дейности
   В дейностите се включват: формулиране на критерии и показатели (експертна дейност); обучение на ученици от 5 клас по темата „геометрични фигури“ (преподавателска дейност); Оценяване на постижения, мотивация, нагласи (експертна дейност).

3. Техники
   В техниките се включват: структуриране на урок с имплементирани елементи за самостоятелно учене; прилагане на подхода на самостоятелното учене в класната стая; обратна връзка и подкрепа на учениците при докладване на резултатите от самостоятелната работа. За трите техники се изисква предварителна подготовка на учителя, който иска да прилага иновативния модел в работата си и следване на алгоритъм описан в технологични решения по-долу.

4. Технологични решения

Технологичните решения на прилагането на иновативния модел следват следния алгоритъм:

• Етап 1: Запознаване с теоретичната рамка – подход за самостоятелно учене
• Етап 2: Планиране на приложението в определен учебен раздел
• Етап 3: Анализ на съдържанието на съществуващите стандартни уроци и преценка къде може да се използва иновативния модел
• Етап 4: Създаване на модифициране уроци с имплементирани задачи за самостоятелно учене отчитащи слаби места в знанията и уменията
• Етап 4. Оценка на началното състояние на знания и умения
• Етап 5. Прилагане на модела в работа в клас (дидактична част);
• Етап 6. Прилагане на модела (резултативна част) Презентиране на решенията на учениците, обратна връзка и подкрепа от страна на учителя
• Етап 7. Оценка на крайното състояние на знания и умения.

 

2. Подходи и средства за верификация на „Модел за ефективно усвояване на съдържанието от раздел „геометрични фигури“ (контролно оценъчна част, приложимост и перспективи)

І. Методи и подходи

За верификацията на модела се използват утвърдени в педагогическата практика методи и подходи:

За верификацията на модела са използвани следните подходи и методи: 1) подходът за апробиране на модела чрез педагогически експеримент; 2) Анкетиране на ученици за отношението им към математиката (раздел геометрични фигури) и математиката изобщо изразяващо се в самооценка на мотивация, нагласи и налични собствени техники за самостоятелно учене;. 3) Оценяване на постиженията на учениците от двете групи включени в педагогическия експеримент с тест за знания (типологично разработен като нормативен тест).

За верификацията на модела се използват следните средства: 1) система от критерии и показатели свързани пряко с изискванията за минимум знания и умения предвидени в ДОС за математика 5 клас. 2) статистически методи и коефициенти за обработка на получените резултати; 3) подход за издигане на нулева и експериментална хипотеза и нейното потвърждаване или отхвърляне, т.е. класически научен подход.

ІІ. Етапи и елементи на верификацията на модела в изследователска перспектива

1. Обект и предмет на изследването. Обект на изследването са знанията и уменията на учениците от пети клас да усвояват учебното съдържание от раздел „Геометрични фигури“ в 5 клас. Предмет на изследването е процеса на усвояването подхода самостоятелно учене, който подобрява възможностите за усвояване на учебното съдържание от раздел „Геометрични фигури“, а към предмета на изследване са и мотивацията на учениците за решават задачи от геометрични фигури и нагласите им към обучението по математика изобщо.

2. Извадка на изследването. Изследването включва прилагане на педагогически експеримент с експериментална и контролна групи. В експерименталната група са включени 15 ученици от 5 клас от СУ „Никола Йонков Вапцаров“, с. Дреновец, общ. Ружинци, обл. Видин. В контролната група са включени 18 ученици от 5 клас от СУ „Никола Йонков Вапцаров“, с. Ружинци, общ. Ружинци, обл. Видин.
3. Хипотези. Хипотезите на изследването представляват конкретизация на общите хипотези представени в увода на разработката. В представения по-долу вид, те имат характера и особеностите на работни хипотези:

Хипотеза 1. След прилагането на модел за ефективно усвояване на съдържанието от раздел „геометрични фигури“ в 5 клас (иновативния модел) при

обучението на учениците от 5 клас (експериментална група) ще се установят: подобрени резултати по знания и умения за решаване на задачи от раздел „геометрични фигури“.

Подхипотеза: Очаква се след прилагането на иновативната технология за експерименталната група да се наблюдава промяна (в тази група) в посока на по-висока мотивация за учене на математика; промяна в посока към по-позитивни нагласи към предмета математика.

Хипотеза 2. Ще се наблюдават различия в резултатите на учениците от експерименталната група по оценката на знания и умения за решаване на задачи от раздел геометрични фигури след прилагането на иновативния модел – учениците с предварително установена нагласа да работят самостоятелно ще постигат по-добри резултати от учениците които нямат такава изградена нагласа.

4. Критерии и показатели

Формулирането на отделните критерии и съответстващите на тях показатели следва от процедурата на операционализация на конструкта съдържащ се в темата на настоящата разработка, а именно: Техники за усвояване на учебното съдържание в раздел „Геометрични фигури“, 5 клас по „Математика“ чрез използване на подхода „самостоятелно учене“.

На първо място са формулирани следните теоретични индикатори (представляващи и Критерии в настоящото изследване) :

1. Знания и умения на учениците по раздел Геометрични фигури в 5 клас (К1)
2. Мотивация за учене на математика раздел „Геометрични фигури“ (К2)
3. Нагласи към предмета математика (К3)
4. Нагласи за самостоятелно учене (К4)
5. Техники за усвояване на учебно съдържание чрез самостоятелно учене (К5)
6. Формулирани са следните показатели към всеки критерий:

 

За критерий 1: 1. Знания и умения за триъгълник и правоъгълник (видове, обиколка, височина и лице) (уроци 92-98) (К1 П1); 2. Знания и умения за успоредник и трапец (видове, обиколка, височина и лице) (уроци 102-110) (К1 П2); 3. Знания и умения за куб и правоъгълен паралелепипед (елементи, развивка, лице на повърхнина, обем) (уроци 113-120) (К1 П3)

За критерий 2: 1. Мотивация свързана с оценките при учене по математика ( учебното съдържание от раздел „Геометрични фигури“) (К2 П1); 2. Мотивация свързана придобиване на знания и умения при учене по математика ( учебното съдържание от раздел „Геометрични фигури“) (К2 П2)

За критерий 3: 1.Утилитарни нагласи (ориентирани към ползите) към предмета математика (К3 П1); 2. Нагласи към предмета математика индуцирани от трудностите (К3 П2); 3. Нагласи към предмета математика индуцирани от семейството (К3 П3)

За критерий 4: 1. Нагласи за самостоятелно учене свързани с личностни особености (К4 П1); 2. Нагласи за самостоятелно учене свързани с изискването на образователната система (К4 П2)

За критерий 5: 1. Собствени техники за усвояване на учебно съдържание чрез самостоятелно учене (К5 П1); 2. Придобити техники за усвояване на учебно съдържание чрез самостоятелно учене (К5 П2)

5. Методики. В рамките на изследването с педагогически експеримент се използват две методики за оценка (приложими на констатиращ и на контролен етап на експеримента):

Методика 1. Анкетна карта за ученици

Анкетната карта с ученици обхваща въпроси отнасящи се до показателите на 4 критерия, а именно: Мотивация за учене на математика раздел „Геометрични фигури“ (К2); Нагласи към предмета математика (К3); Нагласи за самостоятелно учене (К4); 5. Техники за усвояване на учебно съдържание чрез самостоятелно учене (К5). По-конкретно са формулирани по 1 или 2 въпроса за всеки показател, като общо са формулирани 11 въпроса.

Методика 2. Нормативен тест за знания (чек лист)

Дидактическият тест е метод, средство за измерване на резултати от учебно-възпитателната работа, провеждана в училище по установени учебни програми и подчинена на определени цели”(Бижков, 1995: 279). В структурно отношение представлява система от въпроси и задачи, проверяваща в еднакви условия нивото на обученост или готовността за обучение. Дидактическите тестове се разглеждат като нормативни и критериални. Те се различават по еталона. Нормативните тестове са ориентирани към средната норма, получена от изследване в представителна извадка. С тях се установяват индивидуалните постижения на тестирания ученик или група в сравнение с останалите тестирани ученици.

Методиката е изградена като са обособени въпроси за проверка на знанията за всеки от показателите и по въпроси за умения за справяне със задачите, които произтичат от темите в раздел Геометрични фигури. По този начин нормативният тест за знания във вид на чек лист придобива форма с 3 секции по една секция за всеки от показателите.

6. Статистистически методи. Използвани са следните статистически методи: Дескриптивен статистически анализ (честотни и процентни разпределения, мода, медиана, средна величина); Графичен метод (графика); Методи на проверяващата статистика (корелационен анализ, t-test, дисперсионен анализ). Прилагането на статистическите методи изисква представяне на установените резултати в подходяща форма за математическа обработка и анализ –таблична и графична (Кожухарова и кол. 2014).

3. Съдържателна рамка на технология за усвояване на учебното съдържание от раздел „Геометрични фигури“ по математика в 5 клас

Към съдържателната рамка, т.е. към съдържанието на самата иновативна технология се отнасят: „Модифицирани уроци с елементи на самостоятелно учене“.

При построяването на съдържателната рамка на трите урока: урок № 100 – обобщителен за триъгълник и правоъгълник; Урок № 112. Преговорен урок за успоредник и трапец; Урок № 122 – обобщителен за геометрични тела, към предвидените педагогически действия произтичащи от целите и задачите на тези преговорни и обобщителни уроци са добавени по 2 задачи за самостоятелна работа на учениците. Тези задачи имплементирани в общата рамка на урока не от стандартния тип „решете самостоятелно следната задача“, а са провокиращи мисленето на учениците сами да решат проблем, който може да бъде решен чрез използването на знания и умения от геометрични фигури. Идеята на всяка от задачите в трите урока е да развиват самостоятелното търсене на решения на практически задачи, които не са формулирани ясно като задачи, но е видно, че се срещат в практиката и тяхното разбиране и справянето с решенията им са полезни за всеки който знае как да ги реши. Например:

• едната задачата към урок № 122 включва разбиране на това какво е повърхнина на басейн, изчисляване на повърхнината на стените на басейна и очакването ученика да се справи с формулиране на предложение как да се изчисли обема на басейн, който е с форма на паралелепипед с фонтан в него, който има постамент с кубична форма.
• едната задача към урок № 100 провокира интереса към изчисляване на лица на триъгълници, които на пръв поглед не са толкова значими за практиката, а именно лицето на малки прозорци с триъгълна форма; 
• задачата за трапец към урок № 112 насочва интереса на учениците към паметниците и техните постаменти със задачата за това, колко трябва да е лицето на предната страна на постамента на паметника (с формата на трапец) така, че да могат да се разположат максимален брой букети с цветя опаковани в целофан с триъгълна форма.

4. Резултати от изследването на приложението на иновативен модел за техники за усвояване на учебно съдържание от раздел „Геометрични фигури“ 5 клас

За проверка на ефективността на модела е приложен статистическия метод t-test за сравнение на независими извадки (при което се сравняват двете независими извадки експерименталната група и контролната група). Метода е използвал поотделно за да се сравнят резултатите между двете групи на контролния етап на експеримента. Накратко тези резултати показват:

• установява се статистически значима разлика между резултатите на контролната група и на експерименталната група по следните скали на Анкетната карта: нагласи за учене на математика от семейството (t = -3,62; р<0,01), общи нагласи за учене на математика (t = -3,62; р<0,01),; нагласи за самостоятелно учене на математика (t = -2,71; р<0,05),.
• установява се статистически значима разлика между резултатите на контролната група и на експерименталната група по следните скали на Чек лист № 1: „Знания за триъгълници“ (t = -2,34; р<0,05), „Умения за триъгълници“ (t = -3,83; р<0,01), „Умения за правоъгълници“ (t = -3,31;

р<0,01);

• установява се статистически значима разлика между резултатите на контролната група и на експерименталната група по следните скали на Чек лист № 2: „Знания за успоредници“ (t = -2,79; р<0,01), „Умения за успоредници“ (t = -4,15; р<0,01), „Знания за трапеци“ (t = -2,14; р<0,05), „Умения за трапеци“ (t = -3,37; р<0,01),
• установява се статистически значима разлика между резултатите на контролната група и на експерименталната група по следните скали на Чек лист № 3: „Знания за куб“ (t = -3,56; р<0,01), „Умения за куб“ (t = -2,86; р<0,01), „Знания за паралелепипед“ (t = -2,96; р<0,01), „Умения за модели“ (t  = -2,56; р<0,05).

 

И при четирите статистически проверки, при които се установи статистически значима разлика на контролния етап коефициентът t е с отрицателен знак, което означава, че в експерименталната група средните стойности по всички изследвани скали от четирите инструмента (Анкетна карта, чек лист № 1, чек лист № 2, чек лист № 3) са значимо по-високи. Горното е в подкрепа на хипотеза № 1 според която След прилагането на модел за ефективно усвояване на съдържанието от раздел„Геометрични фигури“ при обучението на учениците от 5 клас (в експериментална групата) ще се установят: подобрени резултати по знания и умения за решаване на задачи от раздел „геометрични фигури“ в сравнение с контролната група.

С цел изследване на влиянието на приложения иновативен модел за самостоятелно учене по време на формиращия етап на експеримента върху експерименталната група и по конкретно върху мотивацията и нагласите за учене на математика (изследвани с анкетната карта) е приложен t-test за сравнение по двойки за всяка от скалите на анкетната карта.

Установи се, че съществуват статистически значими разлики в средните стойности на изследваните ученици от експерименталната група по всички скали на Анкетната карта на контролния етап в сравнение с констатиращия етап (при p<0,01 или p<0,05), като коефициентът t навсякъде е с отрицателна стойност, което означава, че при всички скали (мотивация, нагласи от семейството, общи нагласи, нагласи към учене, самостоятелни техники за усвояване) имаме повишаване на самооценката в края на педагогическия експеримент.

Горното е в подкрепа на допълнителната хипотеза към хипотеза 1, че иновативния модел използващ подхода на самостоятелното учене за обучение по математика раздел геометрия – геометрични фигури, в което се твърди, че модела ще повлияе позитивно на мотивацията, нагласите и техниките за усвояване на знания и умения чрез самостоятелно учене.

С цел проверка на втората хипотеза бе приложен регресионен анализ, резултатите от който показаха че учениците с предварително установена нагласа да работят самостоятелно не постигат статистически значимо по-високи резултати от учениците от експерименталната група, които нямат такава нагласа (общо за трите групи геометрични фигури) което означава, че втората хипотеза не се потвърждава. Все пак коефициентът на регресия Beta е достатъчно висок (Beta 0,452 при Sig. =0,091), което  означава, че съществува тенденция за влияние на този фактор (нагласата за самостоятелно учене) върху по-добрите постижения за знания и умения за трите групи геометрични фигури общо.

При проверка за евентуално влияние на нагласите за самостоятелно учене върху всяка група фигури поотделно се установи, че съществува значимо влияние само върху групата: триъгълник/правоъгълник (Beta 0,538 при Sig. =0,039)..За проверка на влиянието на демографския фактор „пол“ върху резултатите на констатиращия е на контролния етап на експеримента за тестовете за знания и умения  използван дисперсионен анализ. Изследвана е само експерименталната група, тъй като те е подложена на формиращото въздействие на иновативния модел. В резултат – не се установиха статистически значими разлики в дисперсиите между половете при изследването по време на констатиращия етап на експеримента (за експерименталната група от ученици от СУ „Н. Й. Вапцаров“, с. Дреновец).

5. Изводи.

В резултат на изследването се потвърдиха хипотеза 1, подхипотезата на първата хипотеза, а хипотеза 2 бе отхвърлена.

Изводите, които могат да се направят са:

• Прилагането на иновативната технология за усвояване на учебното съдържание от раздел „Геометрични фигури по „Математика“ в 5 клас води до по-високи нива на знания и учения на учениците и по трите групи фигури: триъгълник и правоъгълник; успоредник и трапец; куб и паралелепипед;
• Иновативния модел използващ подхода на самостоятелното учене за обучение по математика раздел „геометрични фигури“, повлиява позитивно на мотивацията, нагласите и техниките да усвояване на знания и умения чрез самостоятелно учене;
• Предварителните нагласи за самостоятелно оказват значимо влияние върху подобряване на постиженията на учениците за групата геометрични фигури: триъгълник и правоъгълник.

 

Обобщение

Разработването и прилагането на иновативен модел използващ подхода на самостоятелното учене за обучение по математика раздел геометрия – геометрични фигури (във вид на „технология за по-добро усвояване на ученото съдържание“), има приложно значение за педагогическата практика на учителите преподаващи в 5 клас.

Постигнатите резултати от прилагането на създадената иновативна технология, базирана на съвременните постижения на подхода „самостоятелно учене“ са верифицирани с помощта на проведен пълен педагогически експеримент в две училища в Северозападна България.

Създадената иновативна технология за по-добро усвояване на ученото съдържание базирана на „самостоятелното учене“ може да бъде използвана от всеки учител по математика, който се запознае с модела и предпочете да подобри усвоимостта на учебния материал от учениците от 5 клас, на които преподава.